Langsung ke konten utama

SOLUSI SPL

Solusi SPL
A.PENGECEKAN SOLUSI SPL DENGAN OBE
Untuk menentukan solusi dari SPL dilakukan dengan cara membentuk matrik yang diperluas/diperbesar dari SPL dan melakukan Operasi Baris Elementer (OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam suatu tahapan dengan menerapkan ketiga tipe operasi berikut untuk menghilangkan bilangan-bilangan tak diketahui secara sistematik.
  1. Kalikan persamaan dengan konstanta yang tak sama dengan nol.
  2. Pertukarkan dua persamaan tersebut.
  3. Tambahkan kelipatan dari satu persamaan bagi yang lainnya.
Karena baris (garis horisontal) dalam matriks yang diperbesar beresuaian dengan persamaan dalam sistem yang diasosiasikan dengan baris tersebut, maka ketiga operasi ini bersesuaian dengan operasi berikut pada baris matriks yang diperbesar.
  1. Kalikanlah sebuah baris dengan sebuah konstanta yang tak sama dengan nol.
  2. Pertukarkanlah dua baris tersebut.
  3. Tambahkanlah perkalian dari satu baris pada baris yang lainnya.
Operasi-operasi ini dinamakan Operasi Baris Elementer (OBE).



B.METODE SOLUSI SPL
  • Kaidah Cramer adalah rumus yang dapat digunakan untuk menyelesaikan sistem persamaan linear. Metode ini menggunakan determinan suatu matriks dan matriks lain yang diperoleh dengan mengganti salah satu kolom dengan vektor yang terdiri dari angka di sebelah kanan persamaannya. Metode ini dinamai dari matematikawan Swiss Gabriel Cramer(1704–1752)

Kaidah Cramer tidak efisien untuk sistem dengan lebih dari dua atau tiga persamaan. Kaidah Cramer juga tidak stabil secara numerik, termasuk untuk sistem 2×2.
  • Invers Matriks

Suatu matriks dapat dibalik jika dan hanya jika matriks tersebut adalah matriks persegi (matriks yang berukuran n x n) dan matriks tersebut non-singular (determinan 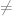\neq 0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
Definisi :
Jika A adalah suatu matriks kuadrat, dan jika kita dapat mencari matriks B sehingga AB = BA = I, maka A dikatakan dapat dibalik (invertible) dan B dinamakan invers dari A
  • Eliminasi Gauss adalah algoritme yang digunakan untuk menyelesaikan sistem persamaan linear. Metode ini dinamai dari matematikawan Carl Friedrich Gauss (1777–1855), walaupun metode ini sudah dikenal oleh matematikawan Tionghoa semenjak tahun 179 M.
    Terdapat tiga jenis operasi yang dapat dilakukan dalam metode ini:
    1. Mengganti urutan dua baris
    2. Mengalikan baris dengan angka yang bukan nol
    3. Menambah suatu baris dengan baris yang lainnya
    Dengan cara ini, matriks dapat diubah menjadi matriks segitiga atas.


  • Eliminasi Gauss Jordan
    Metode eliminasi Gauss-Jordan kurang efisien untuk menyelesaikan sebuah SPL, tetapi lebih efisien daripada eliminasi Gauss jika kita ingin menyelesaikan SPL dengan matriks koefisien sama.
    Motede tersebut dinamai Eliminasi Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Wilhelm Jordan.  
Dalam aljabar linear, eliminasi Gauss-Jordan adalah algoritme versi dari eliminasi Gauss. Pada metode eliminasi Gauss-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (Semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).




TERIMAKASIH TELAH MEMBACA

Komentar

Posting Komentar

Postingan populer dari blog ini

Nilai dan vektor Eigen

Nilai dan vektor Eigen Nilai Eigen ( λ)  adalah nilai karakteristik dari suatu  matriks  berukuran n x n, sementara vektor Eigen (x)  adalah  vektor kolom  bukan nol yang bila dikalikan dengan suatu matriks berukuran n x n akan menghasilkan vektor lain yang memiliki nilai kelipatan dari vektor Eigen itu sendiri. Definisi tersebut berlaku untuk matriks dengan  elemen   bilangan real  dan akan mengalami pergeseran ketika elemen berupa  bilangan kompleks .Untuk setiap nilai Eigen ada pasangan vektor Eigen yang berbeda, namun tidak semua persamaan matriks memiliki nilai Eigen dan vektor Eigen. Nilai Eigen dan vektor Eigen berguna dalam proses kalkulasi matriks, di mana keduanya dapat diterapkan dalam bidang  Matematika murni  dan  Matematika terapan  seperti  transformasi linear . Kumpulan pasangan nilai dan vektor Eigen dari suatu matriks berukuran n x n disebut sistem Eigen dari matriks tersebut. Ruang Ei...
Posting Komentar
Baca selengkapnya

Pengantar Sistem Persamaan Linear (SPL)

SISTEM PERSAMAAN LINEAR Sistem persamaan linear  adalah sekumpulan  persamaan linear  yang terdiri dari beberapa variabel. Contohnya adalah: Sistem ini terdiri dari tiga persamaan dengan tiga variabel  x ,  y ,  z . Solusi sistem linear ini adalah nilai yang dapat menyelesaikan persamaan ini. Solusinya adalah: {\displaystyle {\begin{alignedat}{2}x&\,=\,&1\\y&\,=\,&-2\\z&\,=\,&-2\end{alignedat}}} Kata "sistem" di sini penting karena menunjukkan bahwa persamaan-persamaannya perlu dipertimbangkan bersamaan dan tidak berdiri sendiri. Dalam ilmu matematika, teori sistem linear merupakan dasar  aljabar linear . Aljabar linear sangat diperlukan dalam bidang  fisika ,  kimia ,  ilmu komputer , dan  ekonomi . Contoh Sederhana. Contoh sistem linear yang paling sederhana adalah sistem linear dengan dua persamaan dan dua variabel: {\displaystyle {\begin{alignedat}{5}2x&&...
Posting Komentar
Baca selengkapnya

Transformasi Linear

TRANSFORMASI LINEAR A.      Transformasi Linear Tranformasi linier merupakan dasar dalam telaah aljabar yang berbentuk fungsi. Transdormasi linier yang dimaksud adalah perpindahan dari satu ruang yang biasanya dinamakan dengan domain atau daerah asal ke ruang lain yang dinamakan kodomain atau daerah hasil. Jika F :  V  à   W  adalah sebuah fungsi dari ruang vektor  V  ke dalam ruang vektor  W  , maka F dinamakan transformasi linear jika :        F( u + v ) = F( u ) + F( v ) untuk semua vektor  u  dan  v  di  V Jika F :  V  à  W  adalah sebuah transformasi linear, maka untuk sebarang v1, v2 di V dan   sebarang skalar k1,k2 diperoleh : F(k1v1 + k2v2) = F(k1v1) + F(k2v2)                               ...
Posting Komentar
Baca selengkapnya